Metrology is almost as much about terminology and standardization as it is about actual measurements.
The Joint Committee for Guides in Metrology (JCGM) even provides an International Vocabulary of Metrology or the VIM which serves to provide a common language and
terminology in the field of metrology. Along with it, the Guide to the Expression of Uncertainty in
Measurement or GUM, also curated by JCGM, defines general rules for evaluating and expressing
uncertainty in measurements.
Key to these guidelines are the definitions listed in the image below. You probably stumbled into
these terms many times in the past. Most of these are also covered in many graduate engineering
programs but, going through this list, can you confidently distinguish and describe in exact terms
what each of these definitions means in the domain of metrology? Let’s take a look at their specific
meaning and implementation.

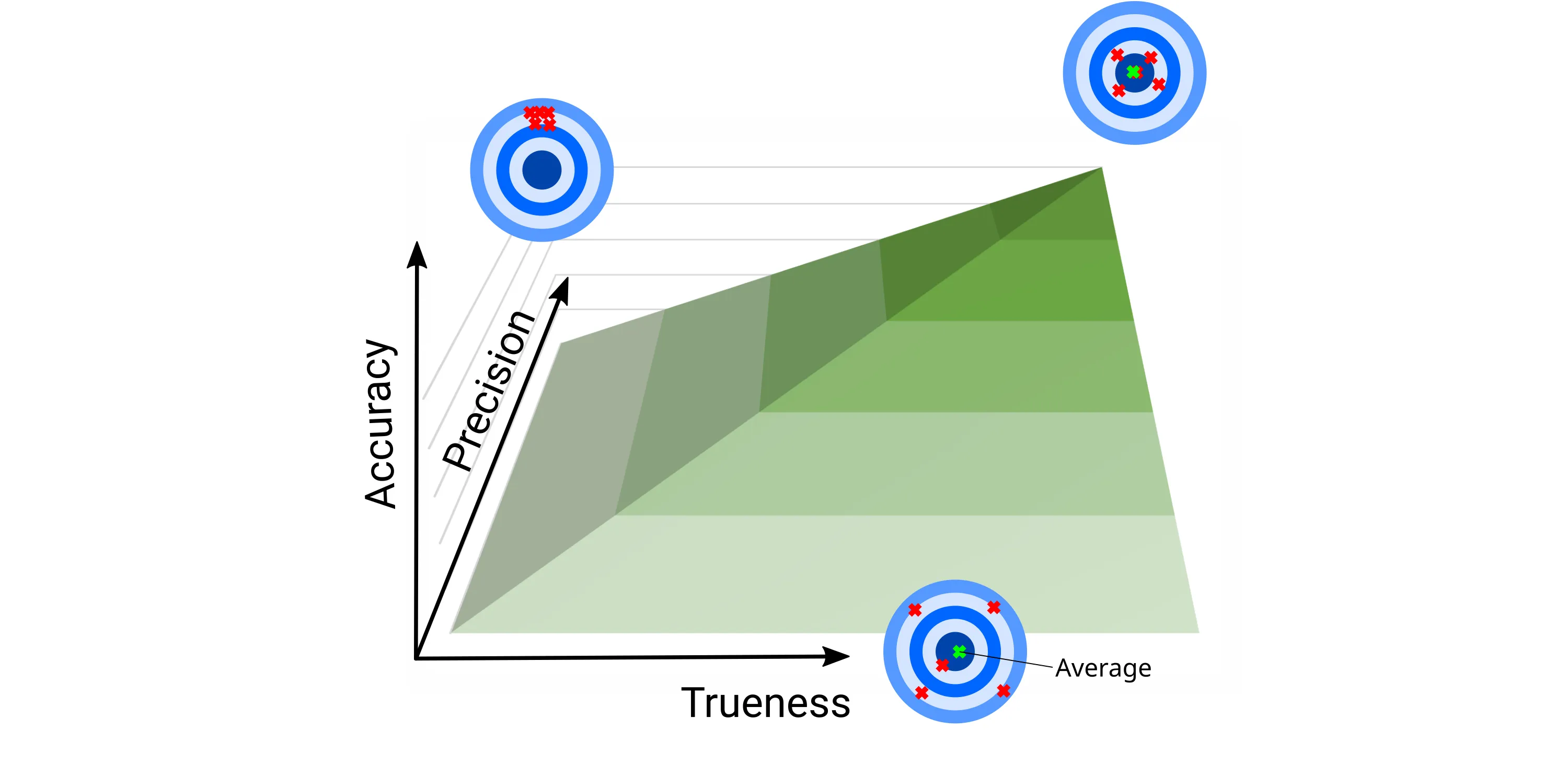
Accuracy
Definition: 'Closeness of agreement between a
measured value and a true quantity value of a measurand.'
Based on this definition, we might think of accuracy as something quite tangible and quantifiable
but, as the VIM notes, measurement accuracy is a
qualitative term, i.e., it is not actually a numerical quantitative value. A measurement is simply
said to be more accurate when it offers a smaller measurement error.
The qualitative nature of the term stems from the fact that the 'true value' in the definition is
never actually known since no reference measurement instrument is infinitely precise and there is
always as small degree of uncertainty remaining about the actual true value. Nevertheless, ISO 5725-1:2023 ---the official
standard defining accuracy, precision, and trueness---accepts that the 'true value' can be replaced
with an 'accepted reference value' (see Reference quantity value section below), making accuracy
quantifiable.
Trueness
Definition: Closeness of agreement between the
average of an infinite number of replicate measured quantity values and a reference quantity value.
Measurement trueness is inversely related to systematic measurement error (see below), but is not
related to random measurement error.
Similar to measurement accuracy, trueness is also a qualitative term since it compares the mean of
actual measurements to a 'true value' which is inherently unknown. Again though, ISO 5725-1, allows to
replace the 'true value' with an 'accepted reference value'.
Precision
Definition: Closeness of agreement between
indications or measured quantity values obtained by replicate measurements on the same or similar
objects under specified conditions.
Measurement precision is a measure of how closely repeated measurements of the same quantity under
the same conditions agree with each other. Precision evaluates the consistency and reliability of a
measurement method. A high-precision measurement system produces closely clustered measurements, while
a low-precision system results in more scattered or variable measurements.
Precision is often used to define measurement repeatability and is expressed using statistical
measures such as standard deviation or variance, which quantify the spread or dispersion of repeated
measurements. It doesn't necessarily guarantee that the measured values are accurate; they can be
consistently off-target.
Repeatability and Reproducibility
Definition: Repeatability and reproducibility are defined as measurement
precision under a set of repeatability or reproducibility conditions of measurement respectively.
We’ve seen that the general term for variability between replicate measurements is precision. When we
want to talk about how precise a measurement method is, we use two conditions: repeatability and
reproducibility. These conditions help us understand how much the measurements can vary in practice.
Repeatability
Under repeatability conditions, we ensure that everything that could change the measurement stays the
same, and we measure how much the results still vary. This helps us understand the smallest possible
variation in the results. To maximize repeatability of your measurements it is recommendable to ensure that:
- The same measurement procedure or test procedure is used
- The same operator performs the measurements
- The same measuring or test equipment is used under the same conditions
- The measurements are done at the same location
- Repetition over a short period of time
Reproducibility
Under reproducibility conditions, we let some or all of the things that could change the measurement
actually vary, and we see how much the results change because of that. This helps us understand the
biggest possible variation in the results.
Other intermediate conditions between these two extreme conditions also occur when one or more of the
factors that influence the measurement are allowed to vary, and are used in certain specified
circumstances
Uncertainty
Definitions:
- 'Non-negative parameter characterizing the dispersion of the quantity values being attributed to a
measurand, based on the information used.' - VIM
- 'Parameter, associated with the result of a measurement, that characterizes the dispersion of the
values that could reasonably be attributed to the measurand' - GUM
Uncertainty of measurement acknowledges that no measurements can be perfect. It is typically
expressed as a range of values in which the value is estimated to lie, within a given statistical
confidence. It does not attempt to define or rely on one unique true value.
The term measurement uncertainty is so broad and absolutely crucial to the field of metrology that it
deserves its own article (or, more likely, a full book) so it will be dealt with in more detail in the
next post.
Measurement error
Definition: measured quantity value minus a
reference quantity value (used as a basis for comparison with values of quantities of the same kind)
Measurement error refers to the difference between a measured value and the true or accepted value of
the quantity being measured. It represents the discrepancy or inaccuracy in a measurement result and
can result from various factors, including equipment limitations, environmental conditions, human
factors, and inherent uncertainties in the measurement process. We can hence think of measurement
error as being inversely related to the measurement accuracy.
Measurement error = Systematic Measurement Error + Random Measurement Error
- Systematic Error: This type of error is consistent and reproducible, affecting all
measurements in a predictable way. Systematic errors result from flaws or biases in the measurement
system or procedure. They can be caused by equipment calibration issues, instrumentation
limitations, or incorrect measurement techniques. Systematic errors often lead to inaccuracies in
the measured values and can be minimized through proper calibration and correction.
- Random Error: Random errors are unpredictable variations in
measurement results that occur from one measurement to another, even when using the same equipment
and following the same procedures. They are typically caused by inherent fluctuations in the system,
environmental conditions, or human factors. Random errors are characterized by their variability and
can be reduced by increasing the precision of measurements, such as using more precise instruments
or averaging multiple measurements.
Reference quantity value
Definition: quantity value used as a basis for
comparison with values of quantities of the same kind
A reference quantity value can be a true quantity value of a measurand, in which case it is unknown,
or a conventional quantity value, in which case it is known.
A reference quantity value with associated measurement uncertainty is usually provided with reference
to:
- material, e.g. a certified reference material,
- a device, e.g. a stabilized laser,
- a reference measurement procedure,
- a comparison of measurement standards.
In the upcoming post we'll take a look more in detail into the definition and methods of evaluation
of uncertainty.
References
[1] The International System of Units (SI) as
defined by BIPM
[2] National Institute on
Standards and Technology (NIST) - Measurement Uncertainty
[3] NIST Uncertainty Machine
[4] NIST/SEMATECH e-Handbook of
Statistical Methods
[5] International
Vocabulary of Metrology
[6]
JCGM 100:2008 GUM 1995 with minor corrections - Evaluation of measurement data — Guide to evaluating
and expressing uncertainty in measurement
Back to blog
Go to next
post


