High-performance plastic gears are increasingly replacing metal gears in various applications
due to their numerous advantages. The main benefits include lower weight, no need for
lubrication, lower cost in mass production, significantly improved NVH (noise, vibration, and
harshness) performance, and superior chemical and corrosion resistance. Most plastic gears are
manufactured using injection molding, which offers exceptional design flexibility. This allows
for the integration of multiple machine elements into a single molded part and enables gear
geometry modifications, such as increased root rounding or customized profile shapes. [1]
Introduction
Plastic gears have been used since the 1960s, when they were initially used for simple motion
transmission applications. Over the years, with the development of new, improved plastic materials,
the technology started to make its way into power transmission applications. Until recently, plastic
gear drives were employed for applications with power up to 1 kW, however, lately, there have been
attempts to use high-performance plastics in gear drives exceeding the 10 kW mark [2].
Along with ever-increasing customer requirements the NVH behavior of polymer gears is also gaining
importance.
The broader adoption of polymer gears could be facilitated if standardized design methodologies were
established and pertinent material information became accessible. Presently, there is a lack of a
global norm that would formalize the calculations, design principles, and recommendations specific
to polymer gears. Certain national standards on this topic do exist, for instance, BS 6168:1987 [3],
as well as the Japanese standard JIS B 1759:2013 [4]. The latter draws from ISO 6336:2006 [5] with
some adaptations detailed in Moriwaki et al.'s study [6]. Additionally, guidelines from diverse
engineering associations are at one's disposal. VDI 2376:2014 [7], a successor to VDI 2545 [8],
published in 2014, stands as the most comprehensive and commonly employed framework for polymer gear
design. It encompasses evaluation techniques for the most recurrent failure modes in polymer gears.
Fundamental material data for substances like POM and PA 66 are also encompassed. AGMA [9,10] has
also issued design guidelines, though these focus solely on potential materials and gear
configurations, neglecting design models and essential material data crucial for polymer gear
design.
Design Rating of Plastic Gears
To ensure a reliable operation of the gearbox each gear needs to be appropriately designed in order
to avoid failure within the required lifespan, working under required operating conditions. Plastic
gears can fail due to different failure modes, i.e. fatigue fracture, wear or plastic deformation,
which is usually thermally induced. Examples of the possible failure modes are shown in Fig. 1. The
fatigue failure mode can result in root fracture (Fig. 1a), flank fracture, or in some cases also
pitting. Out of the three, the most common fatigue failure mode is root fracture, while flank
fracture is often correlated with unfavorable contact characteristics of the gear pair, and pitting
was only observed in some oil lubricated cases. Wear, shown in Fig. 1b is another common failure
mode for plastic gears. The degree of wear the gear exhibits depends on a variety of factors, e.g.
operating temperature, lubrication, load, material of the mating gear, etc… Notable wear of the
flank profile, deviating it from the involute shape, leads to an elevated level of transmission
error and worse NVH performance. As the wear progresses significantly, it also results in the
breaking of teeth, with cracks originating from the worn tooth profile. The acceptable extent of
wear varies depending on the specific use case. In applications demanding high precision (such as
robotics and sensors), minimal wear is permissible, whereas in applications with lower precision
requirements (like household appliances, power tools, and e-bike drives), a relatively substantial
degree of wear is acceptable, involving a reduction in tooth thickness within the range of 20-30% of
the gear module.
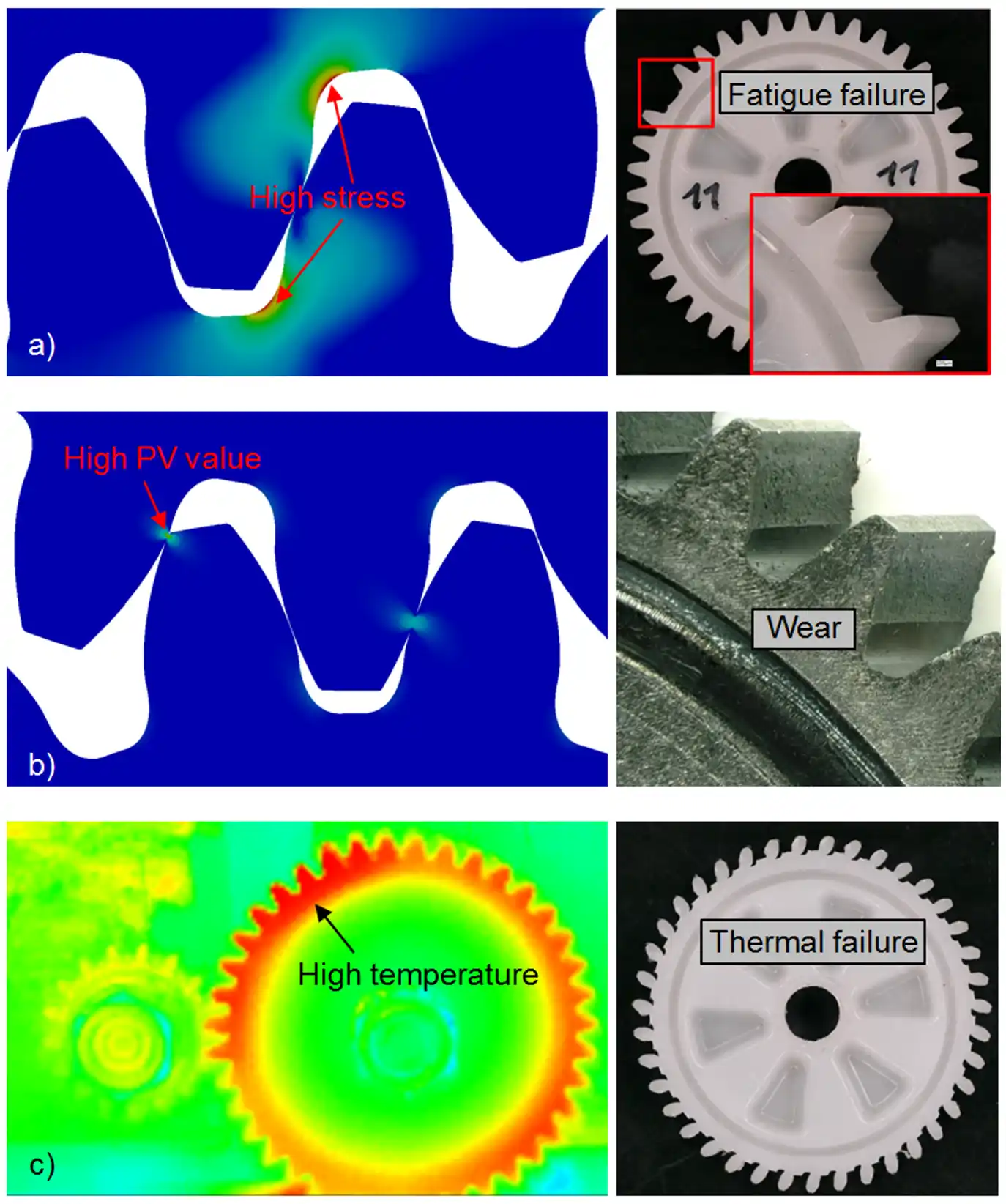
Fig. 1: Possible failure modes for plastic gears: a) root fatigue, b) wear, c) plastic
deformation due to thermal overload.
VDI 2736: Part 2 [7] proposes a framework representing the entire failure mode control process
against each recognized failure mode. While the proposed procedures are feasible, the real problem
arises as each control model requires some gear-specific material data, which is very limited. To
patch this problem, VDI 2736:Part 4 [11] provides testing procedures on how to generate the required
material data.
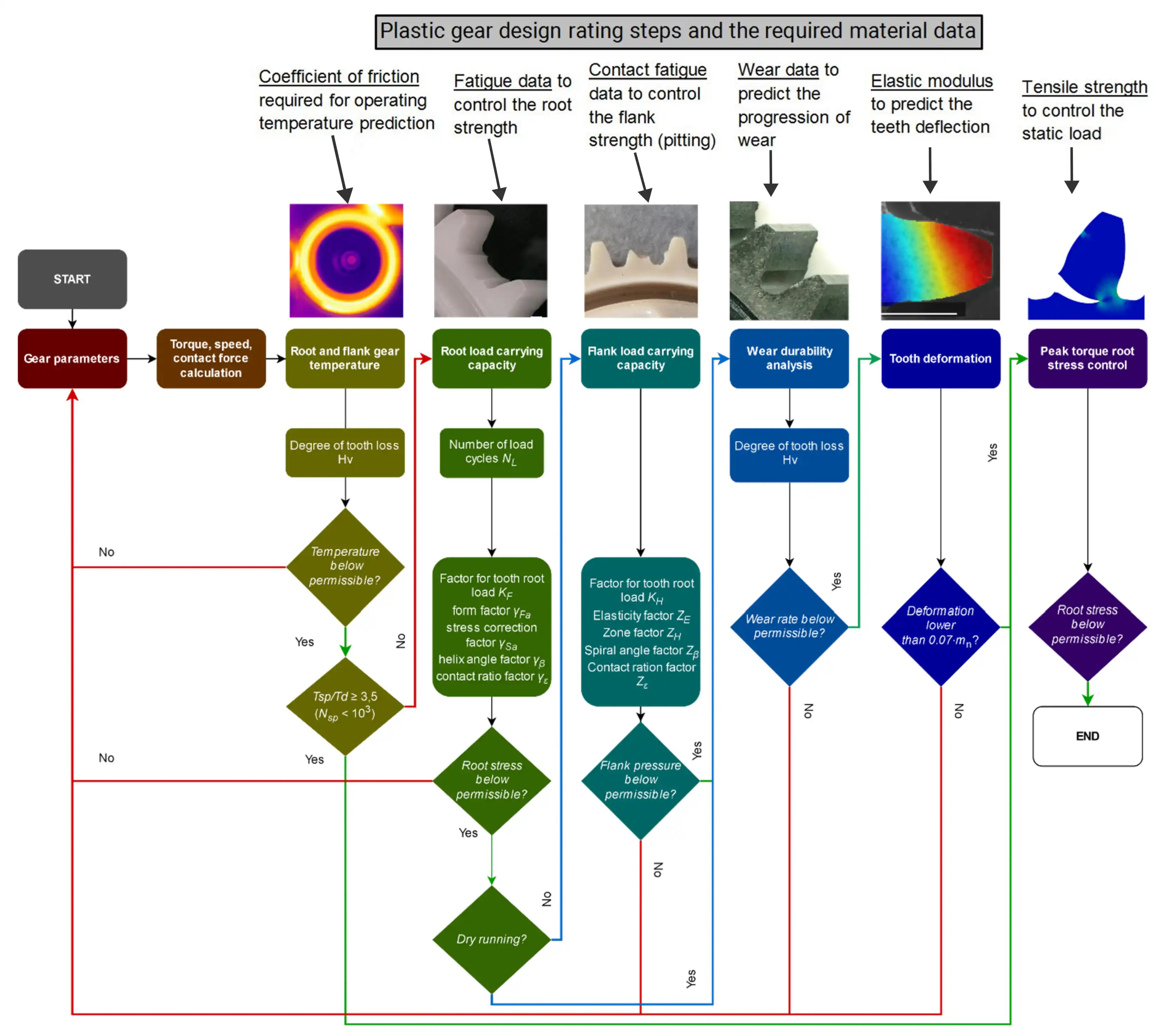
Fig. 2: Failure mode control process within the plastic gear’s design phase as recommended by
the VDI 2736: Part 2 guideline for cylindrical gears.
Step 1. Calculate the operating temperature for the gear pair under design
In order to ensure a reliable operation of a plastic gear, its operating temperature needs to be
lower than the permissible temperature for a continuous load. Coefficient of friction for the
selected material pair is needed in this step in order to be able to calculate the heat generated by
friction.
This step is especially important for applications where gears run continuously at least for some
minutes. Applications where gears run for a few seconds and then stop, do not exhibit a high
temperature increase.
Step 2. Root strength control
The actual stress in the tooth's root needs to be lower as the material's fatigue limit at the
desired number of load cycles (1 rotation of gear is 1 load cycle on each tooth). Knowledge on the
material's fatigue strength is required to complete this step.
As the plastic’s fatigue strength is temperature dependent it is important to rate the calculated
stress in the gear against the material’s fatigue limit determined for the gear’s operating
temperature (usually the temperature calculated in Step 1).
Step 3. Flank strength control against pitting
This step is usually performed only for plastic gear pairs running in oil, which exhibit a high
enough root strength for the root fatigue failure mode not to occur before any pitting is evident.
For the vast majority of plastic gears (dry running or grease lubricated), root fatigue or wear are
the most frequent failure modes.
Step 4. Wear control
Needs to be conducted for dry running plastic gears. It is recommended to do this control step also
for grease-lubricated plastic gears if the plastic material is reinforced with fibers. Pulled-out
and cracked fiber particles tend to mix with the grease forming an abrasive medium.
Wear factor for the material pair of choice is required to conduct this step. Note that wear
behavior of plastics is again temperature dependent hence for design rating purposes a wear factor
characteristic for the operating temperature needs to be applied.
Step 5. Teeth deflection control
Excessive deflection of teeth should be avoided in order to prevent teeth jamming and irregular
meshing. Elastic modulus is required in this step in order to be able to calculate the tooth's
deflection.
Step 6. Control of the static load
In some applications the gears are loaded with a high static load, e.g. holding some weight in a
defined position. In that case the gears need to be rated against a static load and knowledge on
material’s tensile strength is required.
It is not necessary to always conduct all of the design rating steps. From the above presented
procedure Step 1, Step 2 and Step 4 are advised to be always conducted, while others are case
dependent.
Calculating the Plastic Gear's Operating Temperature
Gears heat up during operation. Friction between the meshing teeth and hysteretic effects are the
main reasons for the temperature increase in plastic gears. The rate of the heat generation and the
resulting temperature rise depend on several factors, e.g. torque, rotational speed, coefficient of
friction, lubrication, thermal conductivity, convection, gear geometry, etc. In order to ensure a
reliable operation of a plastic gear, its operating temperature needs to be lower than material’s
permissible temperature for a continuous load.
The first rating point, for plastic gears, is the prediction of the operating temperature in order
to ensure no thermal overload (Fig. 1c) occurs under the specified operating conditions. The VDI
2736 guideline employs here a slightly supplemented Hachmann-Strickle model [12], which was
presented in 1960's. The Hachmann-Strickle model was later supplemented by Erhard and Weiss [13].
The guideline goes further and proposes a model for calculating the temperature in the tooth's root:
\[ \vartheta_{F u \beta} \approx \vartheta_0+P \cdot \mu \cdot H_V \cdot\left(\frac{k_{\vartheta,
\text { Root }}}{b \cdot z \cdot(v \cdot m)^{0,75}}+\frac{R_{\lambda, G}}{A_G}\right) \cdot E
D^{0,64} \]
and on the flank:
\[ \vartheta_{F u \beta} \approx \vartheta_0+P \cdot \mu \cdot H_V \cdot\left(\frac{k_{\vartheta,
\text { Flank}}}{b \cdot z \cdot(v \cdot m)^{0,75}}+\frac{R_{\lambda, G}}{A_G}\right) \cdot E
D^{0,64} \]
Evidently, the equations are almost the same, as there is difference only in one factor, the \[
k_\vartheta \], where the guideline provides different values for the root region and the flank
region. In the proposed equation the most important factor is the coefficient of friction, which is
dependent on several parameters, e.g. material combination, temperature, load, lubrication,
sliding/rolling ratio, siding speed, etc.
The VDI model is analytic and easy to use, while the accuracy of results is limited. Several
scientific studies, e.g. Fernandes [14], Casanova [15], Černe [16], were presented recently which
dealt with this topic and each one proposed different, advanced, numerically-based temperature
calculation procedures.

Fig. 3: a) Thermal image of a Steel/Plastic gear pair during operation, b) Thermal image of a
Plastic/Plastic gear pair.
Root Strength Control
To avoid root fatigue fracture, which is a fatal failure, the root stress σF in a gear
needs to be lower than the material’s fatigue strength limit σFlim for the required
operating lifespan. To account for unexpected effects some additional safety SF is
usually also included.
\[\sigma_\text{F} \leq \frac{\sigma_\text{Flim}}{S_\text{F}}\]
To calculate the root stress the VDI 2736 guideline proposes the same equation as provided by the
DIN 3990 (Method C) [17], which is a standard for steel gears:
\[\sigma_F=K_A \cdot K_V \cdot K_{F \beta} \cdot K_{F \alpha} \cdot Y_{F a} \cdot Y_{S a} \cdot
Y_{\varepsilon} \cdot Y_\beta \cdot \frac{F_t}{b \cdot m}\]
The guideline further simplifies the equation by assuming that for plastic gears, if the condition
b/m\le12 is met, the root load factor can be defined as
\[K_F=K_A\cdot K_V \cdot K_{F\beta} \cdot K_{F\alpha}\approx1\ldots.\ 1.25.\]
While the Eq. 4 is simple to use and familiar to any gear design engineer, the major drawback is
that it does not account for the load induced contact ratio increase, hence overestimating the
actual root stress values. A more accurate root stress calculation can be achieved by employing
numerical manners, e.g. by a FEM simulation. FEM-based methods are however labor and cost intensive.
Assuming the root stress for the gear design under evaluation is calculated, it needs to be
compared to a fatigue limit σFlim, which is a material property and needs to be
characterized by extensive gear testing on dedicated test bench. For plastic materials the
σFlim is temperature dependent, therefore several S-N curves generated at different gear
temperatures are required.
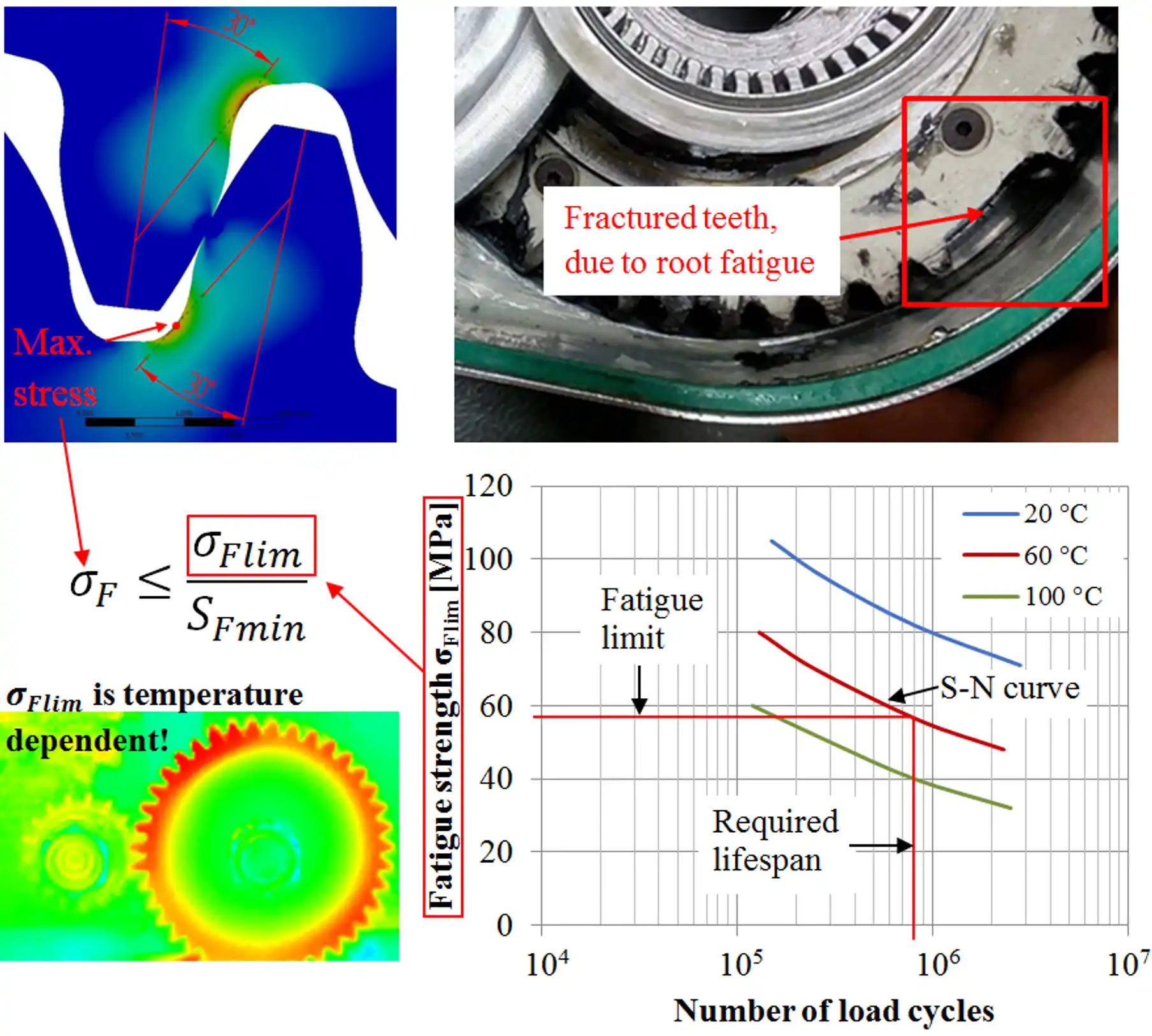
Fig. 4: Temperature dependent S-N curves are needed in order to conduct root strength control.
Flank Strength Control
Flank fatigue failures have been observed mostly in oil-lubricated applications with plastic gears.
Assuming the operating temperature is not exceeding the limit temperature for continuous operation,
in dry running conditions plastic gears usually fail due to root fatigue or wear. Thus for dry
running conditions this step is not included, as it is expected that the wear of flanks will be much
more severe than the flank fatigue. To avoid flank fatigue failure in lubricated contacts, the flank
pressure σH needs to be lower than the material’s fatigue strength limit σHlim
for the required operating lifespan. To account for unexpected effects some additional safety
SH is usually also included.
\[\sigma_H \leq \frac{\sigma_{H l i m}}{S_H}\]
To calculate the flank pressure the VDI 2736 guideline again proposes the same equation as provided
by the DIN 3990 standard:
\[\sigma_H=Z_H \cdot Z_E \cdot Z_{\mathcal{E}} \cdot Z_\beta \cdot \sqrt{\frac{F_t}{b \cdot d_1}
\cdot \frac{u+1}{u} \cdot K_A \cdot K_V \cdot K_{H \beta} \cdot K_{H \alpha}}\]
if the condition b/m
<= 12 is met, the same simplification as in root stress calculation applies also to the flank load
factor
\[K_H=K_A \cdot K_V \cdot K_{H \beta} \cdot K_{H \alpha} \approx 1 \ldots 1.25 .\]
Once the flank pressure for the gear design under evaluation is calculated, it needs to be
compared to a fatigue limit σHlim, which is a material property and needs to be
characterized by extensive gear testing on a dedicated test rig. For plastic materials, again,
the σHlim is temperature dependent, therefore several S-N curves, with flank fatigue
as a failure mode, generated at different gear temperatures are required.
Wear control
Wear is a common damage mode for dry run and also some grease-lubricated applications with
plastic gears. It can lead to a fatal failure where teeth are worn to the degree that they break
instantly under load or that fatigue cracks originates at the worn section. Wear of plastic
gears, in the final stages, leads to fracture (assuming gears are not replaced before). The
crack initiation location in such cases often differs from what is expected as a classic root
fatigue failure mode. Due to the reduced tooth thickness, the stress concentration and
consequently the crack initiation location can be often found higher in the dedendum area, in
the region where the active tooth flank starts. In several applications the gears might not have
failed, however do not fulfill the application requirements if they are worn over an acceptable
degree, e.g. high precision applications. The following equation:
\[W_m=\frac{T_d \cdot 2 \cdot \pi \cdot N_L \cdot H_V \cdot k_w}{b_w \cdot z \cdot l_{F l}}
\leq 0.2 \cdot m_n\]
is proposed by the VDI 2736 guideline for wear control. The only material-dependent parameters
is the wear factor k_w, which considers the wear properties of the material pair under
evaluation. It is important to note that the wear behaviour of plastic gears is dependent on
both materials in pair.

Fig. 5: Severe wear, leading to fatigue induced cracks at the worn section of the tooth
profile, b) Root fatigue failure mode – crack originates in the filleted root section.
Holistic Gear Design Methodology
The above presented gear design rating procedures provide valuable tools which enable to
evaluate gear designs against all possible failure modes. Such rating procedures are of course
possible if all the required material data is available, which usually is not. When starting
with a new gear drive design, utilizing plastic gears, we often face several questions:
1. Which materials to use?
2. Dry run or lubrication (which lubricant to use)?
3. Are we getting the best performance out of the current plastic gear design?
4. Will the gears survive the req. lifespan without decrease of performance or failure?
5. Will the drive’s characteristics and efficiency be as requested?
6. Will the drive’s NVH behavior be satisfactory?
Those questions can be successfully addressed by employing the below presented holistic gear
design methodology. The proposed methodology has several test stages, resulting in a reduced
number of tests and providing reliable material data for the rating procedures of gears for
various applications.
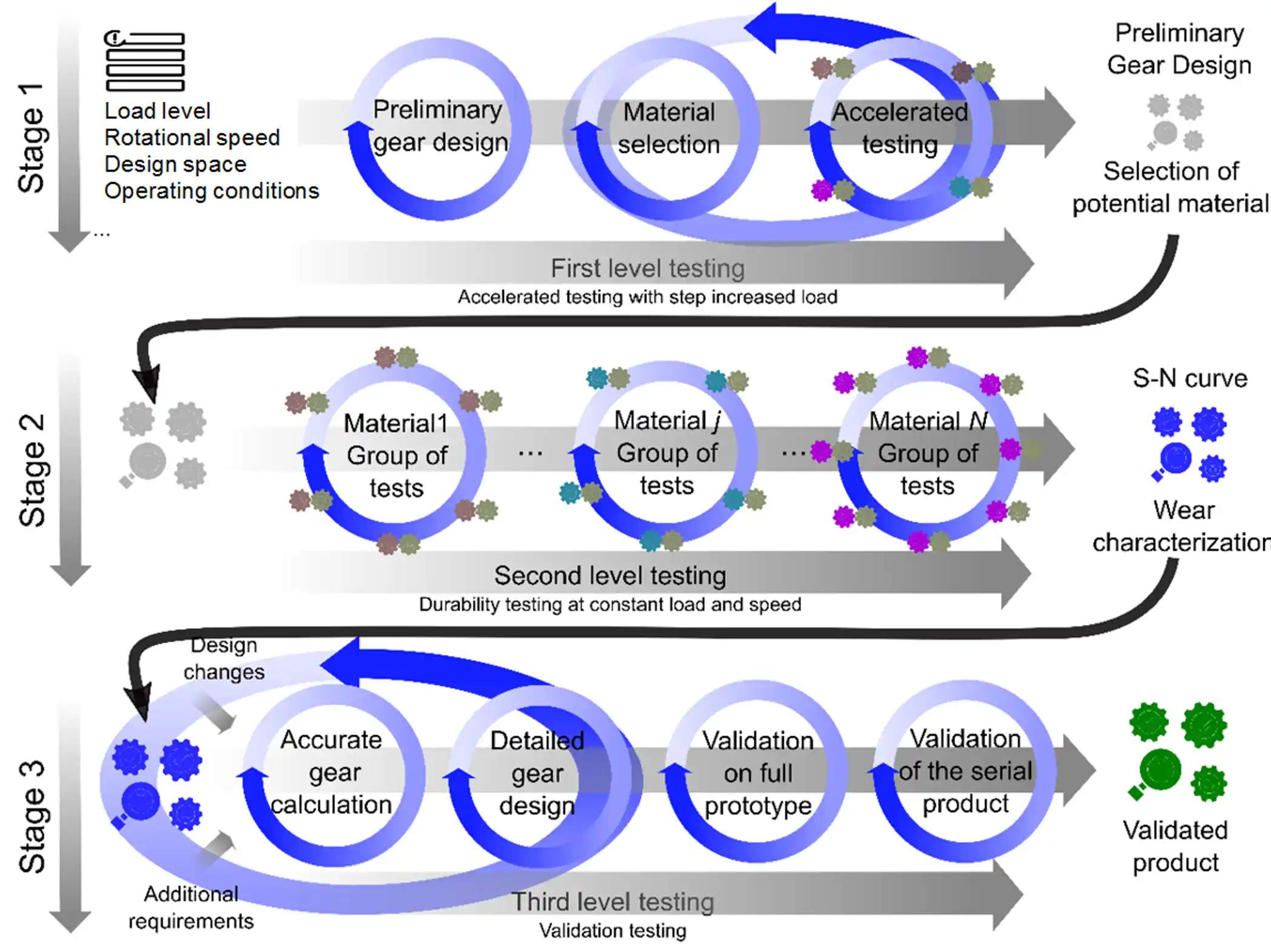
Fig. 6: Holistic development process for gearboxes with plastic gears.
The procedure consists of several steps:
1. Preliminary gear design, based on the input data (material selection, simple design
calculations for the gears). If the selected polymer material pair already has known material
properties, the procedure can be continued with Stage 3.
2. For initial material screening accelerated (step) tests can be employed. These enable to
evaluate a large set of different materials (or material pairs) in a rather quick and cost
efficient way. Such tests need to be conducted at precisely controlled operating conditions.
Usually the torque is increased in steps, until the final gear failure, and the rotational speed
is kept constant. When dealing with plastics the operating temperature is a highly important
parameter. In step tests, there are two possibilities, depending on what the research focus is.
a) If the focus is to compare the material's load bearing capacity under fatigue load, it is
better if the plastic gear's temperature is controlled.
b) If the focus is to study the tribological behavior, it is more convenient to let the gear
pair evolve its own operating temperature. This way, material combinations which exhibit a lower
friction, can be identified. By employing the same approach also different lubricants can be
evaluated and the best one for your gear application can be selected.
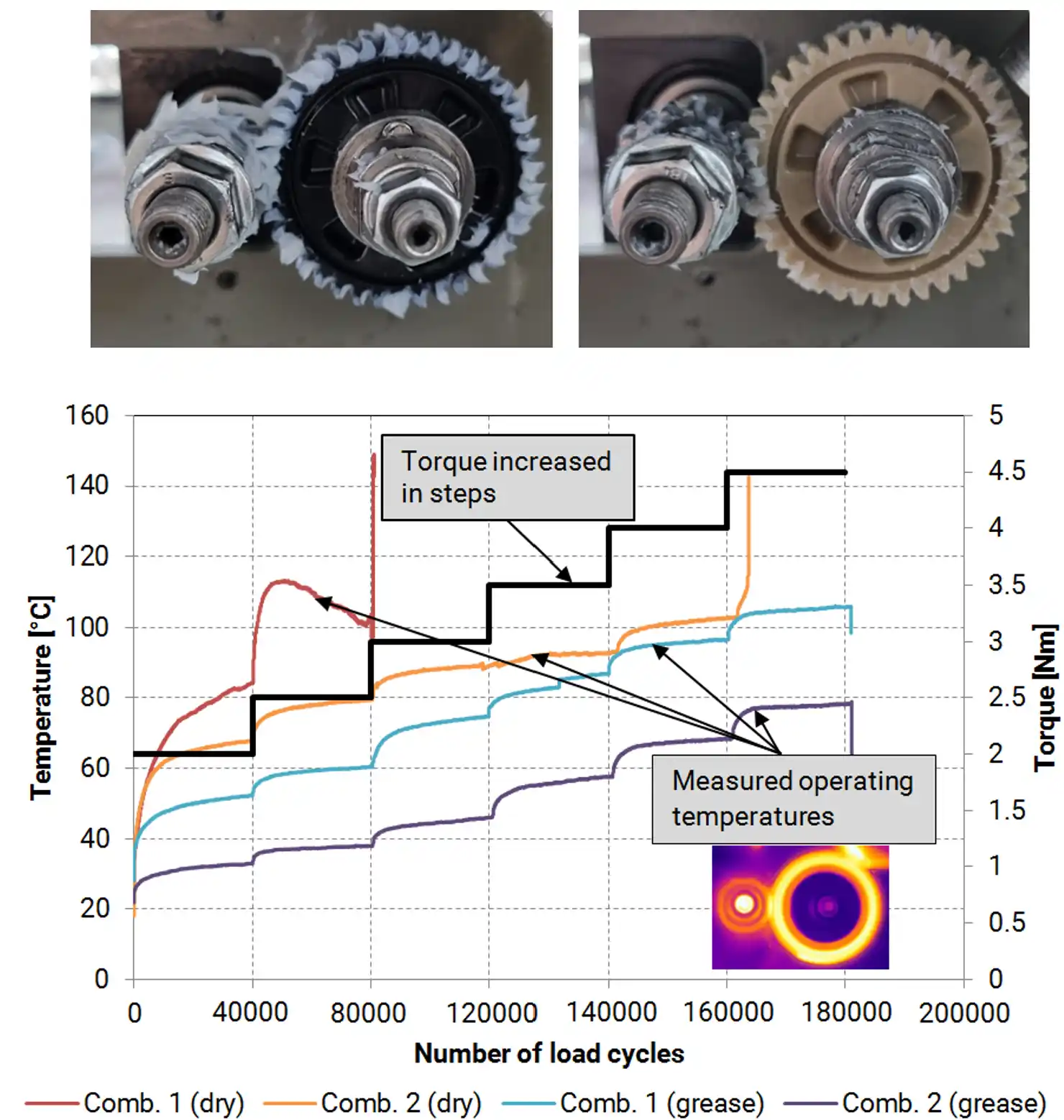
Fig. 7: The accelerated gear testing methodology.
3. When the best performing materials are identified they are further tested to generate S-N
curves and characterize wear factors. Once available, these data enables a reliable and
optimized gear design, with the best possible material utilization.
4. Detailed calculation and design of polymer gears: Well-defined material properties (Stage 2)
enable reliable calculation of gears. This reduces the number of prototypes required.
5. Testing of gears in the final application - product validation. The production of tools for
injection molding is expensive and time-consuming. It is important to do all the previous steps
well and produce the tools only once.

Fig. 8 : Validation on the final application.
Conclusions
Plastic gears offer several advantages over metal gears. With an increase of e-mobility and the
growing demands on the user experience where the NVH needs to be held at a minimum, plastic
gears show great potential. They also provide great benefits in terms of cost optimization and
energy savings.
For reliable design of plastic gears, several different failure modes need to be considered.
The VDI 2736 guideline provides methods and models to control individual failure modes in the
gear design phase. A major problem preventing the use of these methods is the lack of
gear-specific material data, which is required to conduct the required design and control
calculations.
Outlook
The lack of reliable gear-specific material data is still a major problem for the design of
plastic gears. The data currently available in the guidelines and commercial software packages
was in large part generated in a non-consistent way without a traceable and repetitive process.
For generation of reliable material data, a standard is required which would define the test
geometries, sample-production process, sample quality requirements, testing methods and
post-processing of the test data. With the emergence of an international standard and
high-quality material-data generated according to the procedures defined by the standard, the
actual growth potential of plastic gears would be reached.
References
[1] D. Zorko, J. Duhovnik, J. Tavčar, Tooth bending strength of gears with a progressive curved
path
of contact, J. Comput. Des. Eng. 8 (2021) 1037–1058. https://doi.org/10.1093/jcde/qwab031.
[2] S. Reitschuster, C.M. Illenberger, T. Tobie, K. Stahl, Application of high performance
polymer
gears in light urban electric vehicle powertrains, Forsch. Im Ingenieurwesen 86 (2022) 683–691.
https://doi.org/10.1007/s10010-022-00592-0.
[3] BS 6168:1987 Specification for non-metallic spur gears, (1987).
[4] JIS B 1759: Estimation of tooth bending strength of cylindrical plastic gears. Japanese
National
Standard, (2013).
[5] ISO 6336: Calculation of load capacity of spur and helical gears, Parts 1-6, International
standard, (2006).
[6] I. Moriwaki, A. Ueda, M. Nakamura, K. Yoneda, D. Iba, New Japanese Standard JIS B 1759 on
load
capacity of plastic gears, in: Int. Gear Conf. 2014 26th–28th August 2014 Lyon, Elsevier, 2014:
pp.
1172–1178. https://doi.org/10.1533/9781782421955.1172.
[7] VDI 2736: Blatt 2, Thermoplastische Zahnräder, Stirngetriebe, Tragfähigkeitsberechnung. VDI
Richtlinien, (2014).
[8] VDI 2545: Zahnräder aus thermoplastischen Kunststoffen, (1981).
[9] ANSI/AGMA 1106-A97: Tooth Proportions for Plastic Gears, (1997).
[10] AGMA 920-A01: Materials for Plastic Gears, (2001).
[11] VDI 2736: Blatt 4, Thermoplastische Zahnräder, Ermittlung von Tragfähigkeitskennwerten an
Zahnrädern, (2014).
[12] H. Hachmann, E. Strickle, Polyamide als Zahnradwerkstoffe (Polyamides as materials for gear
wheels), Konstruktion 18 (1966) 81–94.
[13] Erhard, G., Weis, C., Zur Berechnung der Zahn- und Flankentemperatur von Zahnrädern aus
Polymerwerkstoffen (On the calculation of tooth and tooth flank temperatures in gear wheels made
of
polymeric materials), Konstruktion 39 (1987) 423–430.
[14] C.M.C.G. Fernandes, D.M.P. Rocha, R.C. Martins, L. Magalhães, J.H.O. Seabra, Finite element
method model to predict bulk and flash temperatures on polymer gears, Tribol. Int. 120 (2018)
255–268. https://doi.org/10.1016/j.triboint.2017.12.027.
[15] V. Roda-Casanova, F. Sanchez-Marin, A 2D finite element based approach to predict the
temperature field in polymer spur gear transmissions, Mech. Mach. Theory 133 (2019) 195–210.
https://doi.org/10.1016/j.mechmachtheory.2018.11.019.
[16] B. Černe, M. Petkovšek, J. Duhovnik, J. Tavčar, Thermo-mechanical modeling of polymer spur
gears with experimental validation using high-speed infrared thermography, Mech. Mach. Theory
146
(2020) 103734. https://doi.org/10.1016/j.mechmachtheory.2019.103734.
[17] DIN 3990: Calculation of load capacity of cylindrical gears, German national standard,
(1987).








