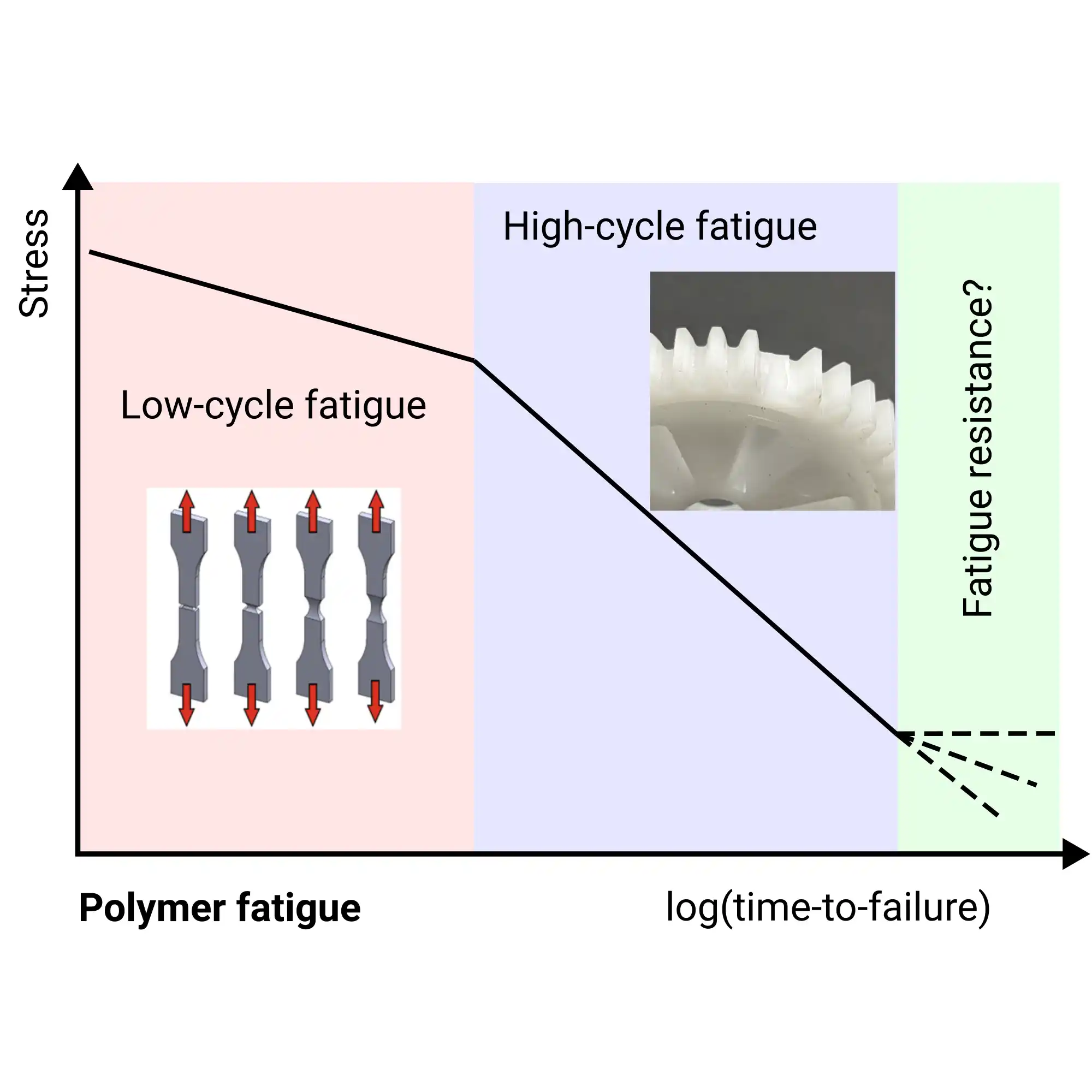
Fatigue failure is a critical concern in the field of structural engineering, specifically in
components subjected to cyclic loading. Understanding and predicting the fatigue life of
load-bearing
components is essential for ensuring the safety and reliability of various structures, from
bridges
and
aircraft to automotive components. Over the years, researchers and engineers have developed
sophisticated models and methodologies to accurately forecast the fatigue life of materials
under
cyclic
loading conditions. In this article, we will delve into the world of fatigue life prediction
models,
exploring various approaches and methodologies employed in structural and mechanical
engineering.
Understanding Fatigue Failure
Before delving into prediction models, it's crucial to understand the concept of fatigue failure.
Fatigue
failure occurs when a material undergoes repetitive loading and unloading, leading to microscopic
cracks
that can propagate and eventually result in catastrophic failure. This phenomenon is particularly
significant in materials subjected to cyclic stresses, such as those experienced by components in
machinery, vehicles, and infrastructure subjected to repeated loading and unloading cycles.
Paris Law: A Classic Approach
One of the pioneering models in fatigue life prediction is the Paris Law, named after Paul Paris
who introduced it in 1961. The Paris Law is an empirical equation that relates the rate of crack growth to the stress intensity factor range. The equation is given by [1]:
\[ \frac{d_a}{d_N} = C(\Delta K)^m \]
where:
- \( {d_a}/{d_N} \) is the crack growth rate per cycle,
- \( \Delta K \) is the stress intensity factor range,
- \( C \) and \( m \) are material constants.
The Paris Law has been widely used for predicting fatigue crack growth in metallic materials, and
its
simplicity and effectiveness make it a popular choice. However, it's important to note that the
constants
\( C \) and \( m \) need to be determined experimentally for each material and loading condition.
Miner's Rule: Cumulative Damage Assessment
While Paris Law deals with crack growth rates, Miner's Rule addresses the cumulative damage caused
by
repeated loading cycles. Developed by M.A. Miner in 1945, this rule assumes that failure occurs when
the
cumulative damage exceeds unity. The equation is expressed as [2]:
\[ \sum \left( \frac{N_i}{N_{f_i}} \right) \geq 1 \]
where:
- \( N_i \) is the number of cycles at stress level \( i \),
- \( N_{f_i} \) is the fatigue life at stress level \( i \).
The left side of the equation calculates the fraction of fatigue life consumed at each stress
level.
When you sum these fractions over all stress levels and the total exceeds 1, it indicates that the
cumulative damage has reached or surpassed the material's fatigue life.
Application
-
Stress Levels: Identify the different stress levels that a material or
structure
experiences during its lifetime.
-
Fatigue Life Data: Determine the fatigue life (\( N_{f_i} \)) at each stress
level
through experimental testing or existing literature.
-
Loading Cycles: Assess the number of loading cycles (\( N_i \)) the material
or
structure encounters at each stress level.
-
Application of Rule: Apply Miner's Rule by summing up the ratios \(
\frac{N_i}{N_{f_i}} \) for all stress levels. If the sum is equal to or greater than 1, it
suggests
that the material or structure is at risk of fatigue failure.
Limitations
While Miner's Rule provides a straightforward and practical method, it has its limitations. One
significant assumption is that damage at different stress levels is independent. In reality,
interactions between stress levels can occur, and this assumption may lead to conservative estimates
of
fatigue life.
Practical Significance
Miner's Rule is especially valuable when dealing with structures subjected to variable loading
conditions over their lifetime. It allows engineers to assess the cumulative damage without the need
for
intricate calculations for each stress level separately.
Advanced Models: Finite Element Analysis (FEA)
With the advancements in computational capabilities, Finite Element Analysis (FEA) has become a
powerful
tool for fatigue life prediction. FEA involves dividing a complex structure into smaller, manageable
elements and solving for stress and strain distributions within each element. The approach provides
a
detailed understanding of the local stress and strain variations, enabling more accurate fatigue
life
predictions.
S-N Curves and High-Cycle Fatigue
The Stress-Life (S-N) approach is commonly used in FEA for high-cycle fatigue analysis. S-N curves
represent the relationship between stress amplitude and fatigue life. These curves are obtained
through
laboratory tests where specimens are subjected to cyclic loading until failure. FEA can then be used
to
correlate real-world stress conditions to the S-N curves, allowing for accurate fatigue life
predictions.
Critical Plane Approach for Multiaxial Loading
Structural components are often subjected to multiaxial loading conditions, where stresses act in
more
than one direction. The Critical Plane Approach, an extension of FEA, is employed to identify the
plane
where fatigue damage is maximized. By determining the critical plane, engineers can make more
accurate
predictions of fatigue life under complex loading scenarios.
Probabilistic Approaches: Weibull Distribution
Probabilistic approaches recognize the inherent variability in material properties and loading
conditions. The Weibull distribution is commonly employed to model the distribution of fatigue life
in a population of identical components. The probability density function of the Weibull distribution is given by [3- 4]:
\[ f(x;\lambda,k) = \frac{k}{\lambda} \left( \frac{x}{\lambda} \right)^{k-1} e^{-(x/\lambda)^k} \]
where:
- \( x \) represents the fatigue life of a component
- \( \lambda \) is the scale parameter
- \( k \) is the shape parameter [5], determining the distribution's skewness and characterizing the
failure behavior.
Interpretation of Parameters
-
Scale Parameter (\( \lambda \)):
- Affects the position of the distribution along the x-axis.
- Larger \( \lambda \) values correspond to longer fatigue life.
- Represents a characteristic life or scale of the distribution.
-
Shape Parameter (\( k \)):
- Influences the shape of the distribution.
- \( k > 1 \) indicates an increasing failure rate over time (wear-out phase).
- \( k < 1 \) suggests a decreasing failure rate over time (infant mortality phase).
- \( k = 1 \) yields an exponential distribution.
Application in Fatigue Analysis
Fitting Experimental Data:
- Engineers often collect fatigue life data through experiments on a group of identical
components.
- By fitting the Weibull distribution to this data, they can model the variability in fatigue life
within the tested population.
Assessing Reliability:
- Reliability engineers use the Weibull distribution to assess the reliability of a system or
component.
- The distribution helps estimate the probability that a component will fail within a certain time
frame.
Shape Parameter Insights:
- The shape parameter (\( k \)) provides insights into the failure characteristics.
- A high \( k \) suggests that most failures occur later in the component's life, while a low \( k
\)
indicates failures are more evenly distributed.
Limitations and Considerations
-
Dependence on Data Quality:
- Accurate parameter estimation relies on high-quality, representative data.
- Outliers or insufficient data can lead to unreliable results.
-
Assumption of Homogeneity:
- The Weibull distribution assumes homogeneity within the tested population.
- If the population is diverse, alternative models might be more suitable.
Practical Significance
The Weibull distribution provides a powerful tool for understanding and modeling variability in
fatigue
life. By applying this distribution to fatigue data, engineers can make informed decisions about the
reliability of components, plan maintenance schedules, and optimize designs for longevity.
Recent Advancements: Machine Learning in Fatigue Life Prediction
As technology continues to evolve, machine learning techniques are being increasingly employed in
fatigue
life prediction. Machine learning models, particularly neural networks, can learn complex
relationships
between various input parameters and fatigue life. These models can account for nonlinearities and
intricate dependencies that may be challenging for traditional analytical methods.
Neural Networks for Fatigue Life Prediction
Neural networks, specifically artificial neural networks (ANNs), have shown promise in predicting
fatigue
life. By training on datasets containing various material properties, loading conditions, and
fatigue
life
data, ANNs can learn to make accurate predictions. This approach is particularly beneficial when
dealing
with complex structures and materials with nonlinear behavior.
Hybrid Approaches: Integrating Analytical Models and Machine Learning
A hybrid approach, combining the strengths of analytical models and machine learning, is gaining
popularity. In this approach, machine learning models are trained using data generated from
analytical
models, enhancing the predictive capabilities. This synergy allows for more accurate fatigue life
predictions while maintaining the interpretability offered by analytical models.
Challenges and Future Directions
Despite significant advancements, challenges persist in accurately predicting fatigue life. One
major
challenge is the need for extensive experimental data to train and validate predictive models.
Obtaining
such data can be time-consuming and expensive, especially for emerging materials and novel
structural
configurations.
Another challenge lies in accounting for environmental factors, such as temperature and corrosive
conditions, which can significantly influence fatigue behavior. Integrating these factors into
predictive
models remains an ongoing area of research.
As we look to the future, the integration of digital twins and real-time structural health
monitoring
could revolutionize fatigue life prediction. These technologies allow for continuous monitoring of
structures, enabling the refinement of predictive models based on real-world performance data.
Conclusion
Fatigue life prediction models play a crucial role in ensuring the structural integrity and safety
of
various components and structures. From classical empirical models like the Paris Law to advanced
finite
element analysis and probabilistic approaches, engineers have a plethora of tools at their disposal.
With
the advent of machine learning, there's a paradigm shift towards more data-driven and accurate
predictions.
As the field continues to evolve, interdisciplinary collaboration between material scientists,
structural
engineers, and data scientists will be paramount. This convergence of expertise will pave the way
for
more
robust and reliable fatigue life prediction models, ensuring the longevity and safety of structures
in
our
increasingly complex and interconnected world.
References
[1] Ewalds, H. L. (1984). Fracture mechanics. 1985 printing. R. J. H. Wanhill. London: E. Arnold. ISBN 0-7131-3515-8. OCLC 14377078.
[2] Y. Kondo, ‘4.10 - Fatigue Under Variable Amplitude Loading’, in Comprehensive Structural Integrity, I. Milne, R. O. Ritchie, and B. Karihaloo, Eds., Oxford: Pergamon, 2003, pp. 253–279. doi: 10.1016/B0-08-043749-4/04029-5.
[3] A. Kızılersü, M. Kreer, and A. W. Thomas, ‘The Weibull Distribution’, Significance, vol. 15, no. 2, pp. 10–11, Apr. 2018, doi: 10.1111/j.1740-9713.2018.01123.x.
[4] Papoulis, Athanasios Papoulis; Pillai, S. Unnikrishna (2002). Probability, Random Variables, and Stochastic Processes (4th ed.). Boston: McGraw-Hill.
[5] R. Jiang and D. N. P. Murthy, ‘A study of Weibull shape parameter: Properties and significance’, Reliability Engineering & System Safety, vol. 96, no. 12, pp. 1619–1626, Dec. 2011, doi: 10.1016/j.ress.2011.09.003.